Tangu

📚 Chapitre : Comprendre les Nombres Réels et Leur Classification

🎯 Objectifs d’apprentissage

À la fin de cette section, les étudiants seront capables de :

• Classer un nombre réel comme naturel, entier, relatif, rationnel ou irrationnel.

• Effectuer des calculs en respectant l’ordre des opérations (PEMDAS).

• Utiliser les propriétés des nombres réels : commutativité, associativité, distributivité, identité et inverse.

• Évaluer et simplifier des expressions algébriques.

---

🧠 Introduction : L’origine des nombres

Les chiffres sont une composante essentielle du langage mathématique. Leur usage remonte à plus de 10 000 ans au Moyen-Orient, où les jetons et cailloux étaient utilisés pour dénombrer du bétail, des grains ou des tissus. Ce système rudimentaire a posé les bases du commerce, de la communication et de la civilisation.

➤ Évolution des concepts :

• Fractions : Introduites par les Égyptiens pour représenter des parts d’un tout.

• Zéro : Ajouté au système de numération vers le 5e siècle en Inde.

• Nombres négatifs : Apparition au 7e siècle en Inde pour représenter les dettes ou pertes.

---

🧮 Classification des Nombres Réels

1. Nombres Naturels

Les nombres utilisés pour compter :

ℕ = {1, 2, 3, 4, …}
Utilisés pour énumérer des objets ou membres (ex : 5 pommes, 12 élèves).

---

2. Nombres Entiers

Les nombres naturels + zéro :

ℕ₀ = {0, 1, 2, 3, …}

---

3. Nombres Relatifs (Entiers positifs et négatifs)

Ils incluent les nombres positifs, négatifs et zéro :

ℤ = {…, –3, –2, –1, 0, 1, 2, 3, …}

Divisés en :

• Entiers positifs (naturels)

• Entiers négatifs

• Zéro (ni positif ni négatif)

---

4. Nombres Rationnels (ℚ)

Tout nombre qui peut s’écrire sous la forme d’une fraction :

a/b où a et b ∈ ℤ, et b ≠ 0
Exemples :

• 1/2, –3/4, 7 = 7/1
  Ils peuvent être écrits avec des décimales finies ou périodiques.

---

5. Nombres Irrationnels

Ne peuvent pas être écrits sous forme de fraction simple.
Leurs décimales sont infinies et non périodiques.

Exemples : √2, π, e

---

6. Nombres Réels (ℝ)

ℝ = ℚ ∪ (nombres irrationnels)
Comprend tous les nombres sur la droite numérique réelle.

---

⚙️ Opérations et Propriétés des Nombres Réels

📐 Propriétés fondamentales :

• Commutativité : a + b = b + a ; ab = ba

• Associativité : (a + b) + c = a + (b + c)

• Distributivité : a(b + c) = ab + ac

• Identité : a + 0 = a ; a × 1 = a

• Inverse : a + (–a) = 0 ; a × (1/a) = 1 (si a ≠ 0)

---

🔍 Évaluer et simplifier des expressions algébriques

1. Évaluer : Remplacer les variables par des nombres et résoudre.

2. Simplifier : Réduire les termes semblables, appliquer les propriétés.

---

🧪 Exemples et Exercices

🔹 Exemple de classification :

Classer –2, 0, 5.75, √2

• –2 ∈ ℤ (entier relatif)

• 0 ∈ ℕ₀ ∩ ℤ

• 5.75 = 23/4 ∈ ℚ

• √2 ∉ ℚ → irrationnel

🔹 Ordre des opérations :

3 + 2 × (5 – 3)²
= 3 + 2 × 4 = 3 + 8 = 11

---

✨ Résumé

Nom	Symbole	Exemples
Nombres naturels	ℕ	1, 2, 3, …
Nombres entiers	ℤ	–2, 0, 5
Nombres rationnels	ℚ	2/3, –1, 4
Nombres irrationnels	—	π, √2
Nombres réels	ℝ	Tous les précédents

---

Souhaitez-vous maintenant un quiz, une fiche d’exercices corrigés, ou une version PDF illustrée de ce contenu pour vos étudiants ?

• Exemples

  Les nombres 3 et 1,5 sont des nombres relatifs positifs.
  Les nombres –3 et –1,5 sont des nombres relatifs négatifs.
  Les nombres +3 et –3 sont des entiers relatifs ; leur partie décimale est nulle.

  Remarque

  Les nombres négatifs sont obligatoirement précédés d'un signe moins (–) dans leur écriture chiffrée usuelle, alors que, pour les nombres positifs, le signe plus (+) est facultatif. 

 

nombre décimal (positif)

Exemples

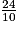2,4 et 3,2 sont des nombres décimaux. On peut les écrire sous forme de fractions décimales : et .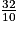

Remarque

Voici une version structurée, pédagogique et illustrée de votre contenu, à intégrer dans un manuel de mathématiques ou une fiche d’apprentissage :

---

📘 Exemples de Nombres Décimaux et Irrationnels

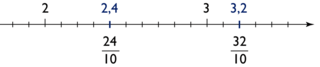
🔹 Nombre Décimal Positif – Illustration 1

Un nombre décimal est un nombre écrit avec une virgule (ou un point en notation anglo-saxonne).
Il possède une partie entière et une partie décimale.

✏️ Exemples :

• 2,4 peut s’écrire comme :

  $$2,4 = \frac{24}{10}$$

• 3,2 peut s’écrire comme :

  $$3,2 = \frac{32}{10}$$

📌 Remarque importante :

Tout nombre entier est aussi un nombre décimal, car il peut être écrit avec une partie décimale nulle.

🔁 Exemples d’équivalences :

• $3 = 3,0 = \frac{30}{10} = \frac{300}{100}$

✅ Conclusion :
Tous les nombres entiers (positifs, négatifs ou zéro) sont des nombres décimaux ayant zéro comme partie décimale.

---

🔹 Nombres Irrationnels – Une autre nature de nombre

À un certain moment de l’histoire, des mathématiciens et constructeurs ont découvert que certains nombres ne pouvaient pas être exprimés par des fractions de deux entiers.

✏️ Exemple concret :

Imaginons un carré de côté 1.
Sa diagonale a une longueur égale à

$$\sqrt{2} \approx 1,4142135…$$

Mais cette valeur ne peut jamais être écrite comme une fraction exacte.

---

🧠 Définition formelle des nombres irrationnels :

Un nombre irrationnel est un nombre réel qui ne peut pas s’écrire sous la forme $\frac{a}{b}$, où $a$ et $b$ sont des entiers avec $b \neq 0$.

Autrement dit :

$$\text{Nombre irrationnel} = \{ h \in \mathbb{R} \ | \ h \notin \mathbb{Q} \}$$

---

🔍 Caractéristiques des nombres irrationnels :

• Leur écriture décimale est infinie et non périodique.

• Ils ne peuvent pas être écrits sous forme de fraction exacte.

✨ Exemples classiques :

Symbole	Nom	Valeur approchée
$\sqrt{2}$	Racine carrée de 2	1,4142135…
$\pi$	Nombre Pi	3,1415926…
$e$	Base des logarithmes	2,7182818…
$\phi$	Nombre d’or (phi)	1,6180339…

---

Tout nombre entier est un nombre décimal.
Par exemple : .


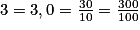Nombres irrationnels À un moment donné dans le passé, quelqu'un a découvert que tous les nombres ne sont pas des nombres rationnels. Un constructeur, par exemple, a peut-être constaté que la diagonale d’un carré comportant des côtés n’était pas égale à 2 ni même à 3/2, mais bien différente. chiffon était un peu plus de 3, mais toujours pas un nombre rationnel. De tels nombres sont dits irrationnels car ils ne peuvent pas être écrits en fractions. Ces nombres constituent l'ensemble des nombres irrationnels. Les nombres irrationnels ne peuvent pas être exprimés sous forme de fraction de deux entiers. Il est impossible de décrire cet ensemble de nombres par une seule règle, sauf pour dire qu'un nombre est irrationnel s'il n'est pas rationnel. Nous écrivons donc ceci comme indiqué. {H | h n'est pas un nombre rationnel}