calcul: dutal Mise en oeuvre de règles de transformation d'une quantité mathématique.
calculer:
utal, Effectuer une opération afin d'obtenir le résultat.
calotte sphérique,
Portion de sphère coupée par un plan sécant à cette sphère.
Si ce plan contient le centre de la sphère, la calotte sphérique est alors appelée un hémisphère.
canonique,
capacité, n. mesure de la contenance d'un récipient.
1.
notations et équivalences
L'unité de mesure de la capacité d'un contenant est le litre (L ou l
lorsqu'il n'y a pas de confusion possible avec le chiffre 1).
2.
Le litre est la capacité d'un contenant dont le volume est de 1 décimètre cube.
3.
Nom
Symbole
Correspondance
litre
L
dm³
décalitre
daL
décilitre
dL
hectolitre
hL
centilitre
cL
kilolitre
kL
m³
millilitre
mL
cm³
mégalitre
ML
dam³
microlitre
µL
mm³
gigalitre
GL
hm³
nanolitre
nL
capital, Montant initial d'argent investi.
caractère,
Propriété, loi, règle qui décrit la spécificité d'un objet mathématique
particulier ou qui permet de vérifier si cet objet possède ou non cette
spécificité.
caractère de divisibilité, n. règle qui aide à déterminer si un nombre est divisible par un autre nombre sans que l'on ait à effectuer la division.
Exemple
Caractère de divisibilité par 5 :
Un nombre est divisible par 5 si le chiffre de ses unités est 0 ou 5.
Un nombre est divisible par 3 si sa somme digitale est divisible par 3.
caractère statistique
Caractère sur lequel
repose une étude statistique. caractère statistique qualitatif
2.Caractère qu'on ne peut associer à un ensemble numérique discret
ou continu.
caractère statistique quantitatif continu, 3. caractère statistique
qui peut prendre toutes les valeurs contenues dans un intervalle réel
donné.
caractère statistique quantitatif discret,
caractère statistique qui peut prendre un nombre fini de valeurs dans
un intervalle donné.
Exemples
Dans une enquête statistique portant sur différents aspects des voyages
effectués par les gens en été, le pays de destination est un caractère
statistique qualitatif.
Dans une enquête statistique portant sur les salaires gagnés par
différents cadres d'entreprises arrondis au millier de dollars près, le
montant des salaires est un caractère statistique quantitatif discret.
caractéristique de dispersion, n. Valeur particulière d'une mesure de dispersion.
caractéristique de position, n. Valeur particulière d'une mesure de tendance centrale.
cardinal d'un ensemble n. Nombre d'éléments d'un ensemble.
carré, n, Figure géométrique plane à quatre côtés d'égale longueur et possédant quatre angles droits. Synonyme de carré géométrique.
carré cartésien n. Produit cartésien d'un ensemble par lui-même.
carré d'un nombre, n. Produit de ce nombre par
lui-même. Le carré d'un nombre n est noté n². Voici la table des carrés
des premiers nombres naturels : 0 1 2 3 4 5 6 7 8 9 10 11 0 1 4 9 16 25
36 49 64 81 100 121
carré géométrique,
Quadrilatère dont les angles sont droits et les côtés isométriques.
Carré Propriétés Le carré a quatre axes de symétrie et un centre de
symétrie. Le carré est un polygone équilatéral et équiangle. Par ses
propriétés, le carré est aussi quadrilatère convexe, un trapèze, un
parallélogramme, un rectangle et un losange.
carré magique,
n.
carré magique, nombres entiers disposés en carré (3 × 3, ou 4 × 4) de
telle sorte que la somme des nombres situés à la verticale, à
l'horizontale et à la diagonale soit toujours la même. Carré magique
Si les nombres entiers utilisés sont consécutifs de 1 à n², on dira
qu'il s'agit d'un carré magique normal.
La somme des nombres sur un même ligne ou une même colonne ou en
diagonale est appelée la somme magique ou la densité du carré magique.
Hétérocarré
d'ordre 4 On appelle parfois carré hétérogène ou hétérocarré une grille
carrée de nombres telle la somme des nombres situés à la verticale, à
l'horizontale et à la diagonale n'est jamais la même.
Si un hétérocarré est formé d'une suite de nombres entiers consécutifs
de 1 à n², on dira qu'il s'agit d'un hérétocarré normal.
On appelle aussi parfois carré antimagique un hétérocarré dans
lequel les sommes des nombres obtenues sur les lignes, diagonales et
colonnes forment une suite de nombres entiers.
carré parfait, n.
Nombre qui est le carré d'un nombre naturel.
Exemples
16 est un carré parfait parce que 4² = 16 et 4 est un nombre naturel.
20 n'est pas un carré parfait car √20 n'est pas un nombre naturel.
Didactique
L'expression « carré parfait » ne doit pas s'appliquer à une expression algébrique quelconque.
Ainsi le trinôme x² - 4x + 4 qui est égal à (x - 2)² ne peut être appelé un carré parfait que si x - 2 est un nombre naturel.
carrelagen. Synonyme de dallage.
cathète, n.
Dans un triangle rectangle, les cathètes sont chacun des deux côtés qui forment l'angle droit.
cathete.gif
Histoire
Dans les traités de géométrie anciens, le terme cathète désignait, d'une façon générale, la hauteur d'une figure.
Gerbert, 10e-11e siècle, dans sa Géométrie :
Un trapèze rectangle est simplement dénommé trapèze. On y distingue la base, la corauste ou petite base et la cathète.
(Voir à ce sujet le très beau site de Thèrèse Eveilleau)
centile,
n
Chacun des nombres qui divisent un ensemble d’observations en 100
parties d'effectifs égaux.
Chacune de ces parties représente ainsi 1/100 de l'échantillon de la
population observée.
Le rang centile correspond à la proportion des valeurs d’une
distribution inférieure ou égale à une valeur déterminée.
Exemple
Si un élève a obtenu une note de 84 % à un test de mathématiques et que
cette note est supérieure ou égale aux notes obtenues par 75 % des
élèves, cela place l’élève dans le 75e centile du groupe observé.
centilitre, Unité de mesure de capacité égale à la centième partie d'un
litre.
centimètre, Unité de mesure de longueur égale à la centième partie d'un mètre.
centimètre carré
centimètre ne cube
centre, gagar, n Point d'un objet caractérisé par la propriété d'être à
une égale distance de l'ensemble des points de cet objet ou de certains
points particuliers de cet objet. igagi, ghaghi
cercle. ,
Courbe plane dont tous les points sont situés à égale distance d'un point donné appelé le centre du cercle.Cercle
La distance qui sépare les points du cercle de son centre est appelée le rayon du cercle.
cercle circonscrit à un polygone, n. cercle qui passe par tous les sommets de ce polygone.
cercle dans un plan cartésien
Lieu de tous les points de coordonnées (x, y) équidistants d'un point fixe appelé le centre du cercle.
Si les coordonnées du centre sont (0, 0), on dit que le cercle est centré à l'origine.
cercle dans le plan géométrique,
figure à deux dimensions dont l'ensemble de tous les points sont situés
à distance égale d'un même point appelé le centre du cercle.
cercle exinscrit à un triangle, cercle tangent aux prolongements des trois côtés d'un triangle.
Dans l'illustration ci-contre, le cercle de centre O est exinscrit au triangle ABC.
cercle inscrit dans un polygone, n
Cercle tangent à chacun des côtés de ce polygone.
cercle unitaire,
dun plan cartésien, cercle de rayon égal à l'unité.
Synonyme de cercle trigonométrique.
grand cercle d'une sphère
Cercle de même rayon que la sphère.
Un grand cercle correspond à la ligne d'intersection entre la sphère et un plan qui passe par le centre de la sphère.
cerf-volant, n
Quadrilatère convexe qui possède deux paires de côtés adjacents isométriques.
Cerfs volants
Lorsqu'un cerf-volant a un seul axe de symétrie (figure de droite, par exemple), on l'appelle parfois pointe de flèche.
chaîne,
Dans un graphe non orienté, suite d'arêtes consécutives. Chaque arête de
la suite a une de ses extrémités en commun avec l'arête précédente et
l'autre extrémité avec l'arête suivante.
Le nombre d'arêtes d'une chaîne détermine la longueur de la chaîne.
chaîne élémentaire, chaîne qui ne passe pas deux fois par le même sommet.
Dans le graphe de droite, la chaîne A-B-C-F-D est une chaîne élémentaire.
chaîne eulérienne, chaîne simple qui passe par toutes les arêtes d'un graphe non orienté.
Dans le graphe de droite, il n'existe pas de chaîne eulérienne parce qu'il y a plus de deux sommets d'ordre impair.
chaîne hamiltonienne, chaîne qui passe une et une seule fois par chacun des sommets d'un graphe non orienté.
Dans le graphe ci-dessus, la chaîne A-B-C-F-E-D est une chaîne hamiltonienne.
chaîne simple,
chaîne qui n'utilise pas deux fois la même arête.
Dans le graphe ci-dessus, la chaîne A-E-F-C-B-A est une chaîne
simple.
chance, dijénge, ani dijénge, il est chanceux.Possibilité qu'un
événement se produise ou d'obtenir un résultat particulier dans une
expérience aléatoire.
changement d'échelle, n.
Dans un plan cartésien, un changement d'échelle peut être obtenu changeant les graduations sur les axes.
chemin,
n nzile
Dans un graphe orienté, suite d'arcs consécutifs. Chaque arc de la suite
a une extrémité en commun avec l'arc précédent et l'autre extrémité
avec l'arc suivant.
Le nombre d'arcs d'un chemin détermine la longueur du chemin ou le
diamètre du chemin.
c
hemin critique, dans un
graphe orienté et valué représentant différentes tâches à réaliser pour
accomplir une tâche, chemin dont la valeur est maximale entre deux
sommets appelés le début et la fin de la tâche.
Dans le graphe orienté et valué présenté à droite, le chemin
critique est le chemin D-1-6-8-9-F qui a une valeur de 14.
chemin élémentaire, chemin qui ne passe pas deux fois par le même sommet.
chemin eulérien
Chemin simple qui passe par tous les arcs d'un graphe orienté.
chemin hamiltonien, chemin qui passe une et une seule fois par chacun des sommets d'un graphe orienté.
chemin simple, chemin qui n'utilise pas deux fois le même arc.
chiffre,
dimeru,
Symbole utilisé pour écrire des nombres.
Dans notre système de numération à base de 10, il y a dix chiffres: 0,
1, 2, 3, 4, 5, 6, 7, 8, 9.
Le système de numération utilisé par les romains de l'Antiquité
utilisait des lettres de l'alphabet latin qui, selon leur position dans
le nombre, avait des valeurs différentes. Les chiffres de ce système et
leurs valeurs respectives sont donnés dans le tableau ci-dessous:
I
V
X
L
C
D
M
1
5
10
50
100
500
1000
Didactique
Il faut veiller à bien distinguer entre chiffre et nombre. Les nombres
s'écrivent avec des chiffres, mais les chiffres ne sont pas des nombres :
on ne peut donc pas les additionner ou les multiplier!
chiffre significatif,
n.
Dans un contexte de mesure, chaque chiffre certain et nécessaire pour
définir cette mesure, ainsi qu'un chiffre incertain évalué par la
personne qui effectue la mesure.
Le chiffre le plus significatif est le premier chiffre d'un nombre, si
ce chiffre est différent de zéro.
Le chiffre le moins significatif est celui, généralement le dernier, qui
est le plus difficile à déterminer. Ce chiffre dépend généralement du
degré de précision de l'appareil de mesure utilisé, des conditions
physiques de la mesure, du soin apporté à la lecture d'une donnée et à
la technique de travail utilisée.
Le nombre de chiffres significatifs d'une mesure ou d'un résultat de
calcul est déterminé dans le contexte de cette mesure ou de ce calcul.
Il s'agit de tous les chiffres de 1 à 9 formant un nombre décimal. Par
convention, le chiffre zéro n'est pas considéré comme significatif s'il
est le premier chiffre du nombre considéré.
Exemples
1,257 comporte 4 chiffres significatifs
5,02 comporte 3 chiffres significatifs
9,08100 comporte 6 chiffres significatifs
0,091 0 comporte 3 chiffres significatifs
3,12 x 10³ est un nombre qui comporte 3 chiffres significatifs.
chronogramme, n.
Diagramme statistique qui sert à représenter les valeurs prises par un caractère qui évolue dans le temps.
Un chronogramme prend généralement l'aspect d'un diagramme à bâtons ou, comme ci-dessus, d'un diagramme à ligne brisée.
circonférence, mesure du tour.
circonférence d'un cercle
Mesure de la ligne courbe qui forme un cercle.
circonférence d'une sphère
Longueur d'un grand cercle d'une sphère.
circuit, dans un graphe orienté, chemin qui commence et se termine au même sommet.
circuit élémentaire
Circuit qui ne passe pas deux fois par le même sommet.
circuit eulérien
Circuit simple qui passe par tous les arcs d'un graphe orienté.
circuit hamiltonien, circuit qui passe une et une seule fois par chacun des sommets d'un graphe orienté.
circuit simple
Circuit qui n'utilise pas deux fois le même arc.
classe,
Élément d'une partition d'un ensemble.
classe d'équivalence
Chaque sous-ensemble induit dans un ensemble par une relation d'équivalence définie dans cet ensemble.
La relation de congruence modulo n dans l'ensemble des nombres entiers est une relation d'équivalence.
classe de reste modulo n
Ensemble des nombres qui ont le même reste par la division par n.
Ces nombres sont dits congrus modulo n.
classe médiane,
classe qui contient la médiane dans une distribution d'une variable
statistique quantitative continue dont les valeurs sont regroupées en
classes de même dimension.
classe modale,
classe dont l'effectif est le plus élevé dans une distribution d'une
variable statistique quantitative continue dont toutes les valeurs sont
regroupées en classes de même dimension.
classe statistique,
chacun des intervalles successifs en lesquels est partagé l'intervalle
total de variation d'une variable statistique quantitative. La grandeur
de ces intervalles est appelée l'amplitude de la classe statistique.
classement, n Répartition d'objets ou de nombres d'après certains
attributs ou certaines caractéristiques.
classification, n. action de classer.
Synonyme de classement.
coefficient, n
coefficient d'un monôme
Constante littérale ou numérique qui multiplie la variable
considérée.
coefficient de corrélation linéaire
Valeur numérique qui caractérise le lien - sens et importance - qui
existe entre deux variables aléatoires ou deux variables statistiques.
coefficient de proportionnalité
Dans des suites proportionnelles, nombre par lequel il faut
multiplier un terme de la première suite pour obtenir le terme de même
rang de la deuxième suite.
coefficient de variation d'une population (statistique)
Mesure de dispersion des données d'une population, égale à (s x
100)/m où s désigne l'écart type et m la moyenne de la série de données.
combinaison,
n.
Dans un ensemble E comprenant n éléments, tout sous-ensemble de E
comprenant k éléments.
Dans une combinaison, l'ordre des éléments n'intervient pas.
Combinaison sans répétition ou sans remise
Synonyme de combinaison.
Combinaison avec répétition ou avec remise
Combinaison des éléments d'un ensemble E dans laquelle les
répétitions (ou remises) sont autorisées et où l'ordre des éléments
choisis n'intervient pas.
Exemples
Soit l'ensemble E = {2, 4, 6, 8}.
Voici quelques exemples de combinaisons des éléments de E pris 2 à la
fois:
{2, 4}, {2, 8}, {6, 8}, {4, 8}.
Voici quelques exemples de combinaisons des éléments de E pris 2 à la
fois avec répétitions:
{2, 4}, {2, 2}, {6, 8}, {4, 4}.
Les sous-ensembles {2, 8} et {8, 2} représentent la même combinaison.
Formulaire
Le nombre de combinaisons des n éléments d'un ensemble E pris k à la
fois est donné par la relation suivante:
combinaison
linéaire, n
Somme de produits d'éléments d'un ensemble V d'objets mathématiques par
des éléments d'un ensemle S de scalaires.
Exemple
Si les variables x et y appartiennent à un ensemble de nombres réels et
que a et b sont des nombres entiers, alors l'expression
z = ax + by
représente le nombre réel z sous la forme d'une combinaison linéaire des
nombres entiers a et b.
Didactique
La notion de combinaison linéaire réfère à deux ensembles V et S
d'objets mathématiques tels, d'une part, des vecteurs d'un espace
vectoriel et, d'autre part, des nombres ou scalaires d'un espace
numérique tel que l'ensemble des nombres réels. On définit alors une
opération externe telle que tout élément de V puisse être exprimé comme
une somme de produits d'un scalaire de S et d'un vecteur de V. Le
nombre de termes de ce produit dépend de la dimension de l'espace
vectoriel choisi. Si l'espace vectoriel est de dimension 2, alors
chaque combinaison linéaire comportera 2 termes; si l'espace vectoriel
est de dimension 3, alors que combinaison linéaire comportera 3 termes.
Et ainsi de suite.combinatoire,
Partie du calcul des probabilités qui traite des procédés de
dénombrement.
Voir aussi :
Arrangement
Combinaison
Permutation
commutativité, n
commutativité
Propriété d'une opération qui permet de changer l'ordre des termes sans
changer le résultat.
Exemples :
L'opération d'addition dans l'ensemble de nombres réels est une
opération commutative. En effet:
∀ x, y ∈ : x + y = y + x.
La composition des translations du plan est un opération commutative.
L'addition des fonctions définies dans est une opération commutative.
La soustraction des nombres entiers est une opération non commutative.
compas, n. Instrument qui sert à tracer des cercles, à construire des angles et à reporter des longueurs.
complémentaire d'un ensemble,
n
Dans un référentiel U, le complémentaire de l'ensemble E est l'ensemble
des éléments qui n'appartiennent pas l'ensemble E.
Le complémentaire de l'ensemble E est noté E'.
Exemple:
E' = {0, 1, 2, 3, 4}
composition de fonctions, n
Étant donné une fonction f, définie de E dans F, et une fonction g,
définie de F dans G, la composée de f et g est la fonction définie de E
dans G qui applique tout élément x de E sur g(f(x)).
La composée des fonctions f et g (soit f suivie de g) est notée g o f
(lire « g rond f »).
Exemple
Soit une fonction f définie par la relation f(x) = x² (représentée ici
en vert) et une fonction g définie par la relation g(x) = sin(x)
(représentée ici en orangé).
La composée g o f est définie par la relation g(f(x)) = sin(x²). Son
graphique est représenté ici en rouge.
concave, n. Synonyme de non convexe.
concavité,
n.
Partie d'un objet ayant une forme creuse ou incurvée vers l'intérieur.
Exemples
Le graphique de la fonction polynômiale du second degré définie par la
relation f(x) = ax² a une concavité tournée vers le haut lorsque le
coefficient a prend une valeur positive, et tournée vers le bas quand le
coefficient a prend une valeur négative.
Graphique de la fonction f définie par la relation y = x²
Une lunule est une surface concave.
concentriques, n. Qui ont le même centre.
conditionnelle,
n.
Relation entre deux formes propositionnelles P et Q, notée « P → Q » ou «
si P alors Q », qui est fausse seulement si l'antécédent P est vrai et
le conséquent Q est faux.
Synonyme de forme propositionnelle conditionnelle.
cône,
n. Solide limité par une surface conique et par un plan qui ne passe
pas par le point de rencontre des génératrices, appelé l'apex du cône.
cône droit,
Si la figure qui lui sert de base a un centre et que le segment
joignant l'apex à ce centre est perpendiculaire au plan qui contient la
base, alors le cône est droit.
cône oblique, cône qui n'est pas droit.
cône tronqué,
l'un des solides obtenus en coupant un cône par un plan non parallèle à
sa base et qui rencontre toutes les génératrices. Le cône tronqué est
celui des deux solides obtenus qui ne contient pas l'apex.
congruence de figures géométriques,
n. Relation par laquelle deux figures peuvent être amenées à coïncider
parfaitement l'une sur l'autre par une isométrie directe.
congruence de nombres, n.
congruents,
n.
Deux nombres entiers sont dits congrus modulo n si leur différence est
un multiple de n, n étant un nombre entier.
On peut aussi dire que deux nombres entiers sont dits congrus modulo n
s'ils ont même reste par leur division euclidienne par n.
En arithmétique modulaire modulo n, les résultats des opérations sont
exprimés modulo n.
Exemples
15 et 3 sont congrus modulo 12. En effet, leur différence, 12, est un
multiple de 12.
Aussi le reste de la division de 15 et de 3 par 12 est 3 dans les deux
cas.
Dans l'arithmétique modulo 5, on peut écrire : 3 + 4 = 2, puisque 3 + 4 =
7 et 7 est congru à 2 modulo 5.
On peut aussi écrire: 3 + 4 congruence.gif 2 modulo 5.
Notation
La relation de congruence modulo n est noté par le symbole:
congruence.gif.
conique, n
Terme général qui désigne une courbe plane obtenue par l'intersection
d'une surface conique de révolution et d'un plan.
Ces courbes, représentées dans un plan, sont appelées des courbes
algébriques. Il s'agit alors du lieu des points d'un plan dont le
rapport des distances à un point (foyer) et à une droite (directrice) de
ce plan est une constante (excentricité).
Ainsi, une conique est l'ensemble des points P tels que le rapport
mes(PF)/mes(PH) = k où H désigne la projection orthogonale de P sur la
directrice d. Le nombre k est appelé excentricité de la conique.
Les courbes algébriques, communément appelées des coniques, sont le
cercle, l'ellipse, la parabole et l'hyperbole.
conjecture,
conjecture
Énoncé qu'on accepte comme vrai mais dont on ne connaît pas la valeur de
vérité parce qu'on ne l'a pas encore démontré ou refuté.
Un conjecture peut être utilisée comme hypothèse d'une démonstration.
Dans une démonstration mathématique, une conjecture est parfois appelée
une hypothèse ou un postulat.
Exemple
La conjecture de Goldbach énonce que tout nombre naturel pair supérieur à
2 peut s'exprimer comme la somme de deux nombres premiers.
Exemples :
4 = 2 + 2
6 = 3 + 3
8 = 3 + 5
Cette conjecture n'a toujours pas été démontrée.
conjonction,
n La conjonction de deux propositions P et Q est la proposition notée P
∧ Q ou « P et Q » qui est vraie lorsque les propositions P et Q sont
simultanément vraies et fausse si l’une des deux propositions est
fausse.
connecteur, n.
En logique mathématique, symbole utilisé pour créer de nouvelles
propositions à partir de propositions données ou de nouvelles formes
propositionnelles à partir de formes propositionnelles données.
Les principaux connecteurs utilisés en logique mathématique sont :
le connecteur de la conjonction : et, symbolisée par ∧
le connecteur de la disjonction : ou, symbolisée par ∨
le connecteur de la négation : non, symbolisée par
le connecteur de la conditionnelle : si ... alors ou implique,
symbolisée par →
le connecteur de la biconditionnelle : équivaut à, symbolisée par ↔
le connecteur de l'identité ou équivalence : si et eulement si,
symbolisée par ⇔
le connecteur de l'implication : entraîne, symbolisée par ⇒
consécutifs, n Qui se suivent.
conséquent,
n.
Ce qui suit, ce qui résulte de ou conclusion dans un raisonnement.
En logique mathématique, second des deux termes d'une forme
propositionnelle conditionnelle ou d'une implication.
Exemple
Dans l'énoncé « si un quadrilatère a une paire de côtés parallèles,
alors ce quadrilatère est un trapèze », le conséquent est la proposition
« ce quadrilatère est un trapèze »
constante
Terme qui désigne certains nombres remarquables (coefficient, rapport,
etc.)
constante de proportionnalité,
Dans des suites proportionnelles, rapport d'un terme de la première suite
au terme de même rang de la deuxième suite.
Synonyme de rapport de proportionnalité.
constante mathématique
Il existe certains nombres dits constants qui correspondent à des
résultats obtenus par calculs ou déductions et qui jouent un rôle très
important dans diverses théories mathématiques.
C'est le cas du nombre π qui représente le rapport de la
circonférence d'un cercle à son diamètre et dont une valeur approchée
est 3,141592.
Le nombre réel e dont une valeur approchée est 2,718 281 8 est la
base des logarithmes naturels ou népériens.
Le nombre d'or, habituellement représenté par la lettre grecque φ,
est aussi une constante mathématique dont une valeur approchée est
1,618.
contour, n.Limite extérieure d'un solide
ou d'une figure plane.
contraction, lorsque deux figures F et F' sont semblables, on dit que
F' est une contraction de F si le rapport de similitude r de F' à F est
compris entre -1 et 1 tout en étant non nul.
contradiction,
n.
Proposition logique composée toujours fausse, quelles que soient les
valeurs de vérité de ses composantes.
Synonyme de proposition toujours fausse.
convexe,
polygone convexe
Polygone dont tous les côtés sont contenus dans le demi-plan limité
par une droite passant par n'importe lequel de ses côtés.
solide convexe
Voir Solide convexe
convexité, Partie d'un objet ayant une forme bombée, saillante ou
incurvée vers l'extérieur.
coordonnées à l'origine,
Dans un plan cartésien, coordonnées des intersections d'une courbe avec
les axes.
Exemple
Dans le graphique cartésien ci-dessus les coordonnées à l'origine de la
droite représentée en rouge et dont l'équation est 4x - 2y + 1 = 0 sont
(- ¼, ½).
coordonnées d'un point, coordonnées
d'un point
n-uplet de nombres qui servent à déterminer la position de ce point dans
un système de repérage dans un plan, tel qu'un graphique cartésien, ou
dans l'espace, tel qu'un système de coordonnées polaires.
Coordonnées cartésiennes d'un point,
dans un graphique cartésien d'ordre n, n-uplet de nombres qui servent à
déterminer la position de ce nombre par rapport à chacun des axes.
Les valeurs sur chacun des axes sont déterminées par projections
parallèles du point sur chacun des axes.
Coordonnées polaires d'un point dans un plan, dans un système de repérage polaire plan,
coordonnées formées d'un couple (r, θ) associées à la position d'un point P, où r désigne la distance de l'origine au point P et θ l'angle de rotation..
CoordPolaires.jpg
L'origine du système de repérage porte le nom de pôle.
La distance du pôle au point P s'appelle le rayon ou l'axe polaire.
L'angle de rotation θ porte le nom d'angle polaire ou d'azimut.
coplanaires, Qui appartiennent à un même plan.
corde, n.
Segment de droite qui joint deux points d'un arc de courbe.
cornet, n Solide constitué d'un cône droit joint à sa base à une demi-sphère de même diamètre.
corollaire,
n. Dans un raisonnement mathématique, énoncé qui résulte immédiatement
d'une proposition déjà démontrée, comme conséquence évidente.
corps, n.
Nom donné à une structure algébrique (K, ⊕ , ⊗) formée d'un ensemble K
dans lequel deux opérations notée ici ⊕ et ⊗ sont des lois de
composition internes répondant aux conditions suivantes :
(K, ⊕) forme un groupe commutatif;
(K*, ⊗) forme un groupe dans lequel K* est formé de tous les
éléments de K sauf l'élément neutre de (K, ⊕);
L'opération ⊗ se distribue sur l'opération ⊕.
Exemple
Les ensembles et munis des opérations + et x sont des corps dont les
éléments neutres sont respectivement 0 et 1.
corps commutatif, corps dans lequel la seconde loi de composition ⊗ est aussi commutative.
corps ordonné, corps dans lequel on peut définir un ordre total compatible avec chacune des lois de composition ⊕ et ⊗.
corps rond, Nom donné généralement au cône, au cylindre et à la sphère.
corrélation,
n.
Lien ou relation de dépendance entre deux phénomènes de nature
statistique ou probabiliste.
Le modèle mathématique qui correspond à ce lien permet de définir une
corrélation linéaire (si le graphique du modèle général est une droite),
une corrélation quadratique (si le graphique du modèle général est une
parabole), une corrélation exponentielle (si le graphique du modèle
général est une courbe exponentielle), etc.
corrélation linéaire,
n
Modèle mathématique qui caractérise le lien ou la relation de dépendance
entre deux phénomènes de nature statistique ou probabiliste dans
laquelle on observe que les couples de données semblent se rassembler
autour d'un droite.
Cette droite porte le nom de droite de régression.
Une corrélation linéaire positive correspond à une corrélation dont
la droite de régression a une pente positive.
Une corrélation linéaire négative correspond à une corrélation dont
la droite de régression a une pente négative.
Une corrélation linéaire nulle correspond à une absence de
corrélation.
correspondants, n.
Angles de même mesure dans des figures semblables ou congruentes.
Voir aussi
Angles correspondants
cosécante d'un angle, n. Inverse du sinus de cet angle.
cosinus d'un angle,
Mesure algébrique de la projection orthogonale sur l'un des côtés d'un
angle de mesure x d'un vecteur unitaire porté par l'autre côté de
l'angle.
sinusoide.jpg
Lorsqu'on associe à un nombre réel quelconque le cosinus de l'angle dont
la mesure, dans le système circulaire, est ce nombre, on définit ainsi
une fonction circulaire appelée fonction cosinus.
Représentation graphique de la fonction f(x)= cos(x) d'amplitude 1 et de
période 2π.
cotangente d'un angle, n. Inverse de la tangente de cet angle.
côté.,
\
Côté d'un angle
Chacune des demi-droites qui déterminent un angle.
Côté d'un polygone
Segment de droite qui forme la frontière d'un polygone.
cote Z (ou cote standard) d'une donnée, Caractéristique statistique
d'une donnée statistique x égale à , où m est la moyenne arithmétique et
σ est l'écart type de la série statistique.
côtés adjacents, n.
Dans une figure géométrique, segments qui ont une extrémité commune.
couche sphérique, n.
Partie d'une sphère comprise entre deux plans sécants parallèles.
couple, n-uplet comportant deux éléments.
couples
réciproques, n.
Couples dans lesquels l'origine du premier est l'extémité du second et
l'extrémité du premier est l'origine du second.
Synonyme de couples symétriques.
Exemple
Les couples (a, b) et (b, a) sont réciproques l'un de l'autre.
On dit aussi le le cou, nple (a, b) est le couple réciproque du couple
(b, a).courbe, ngotu, dingotu, courbe, chemin, virage, nzile jiji
mangotu, le sentier est tortueux
.Nom général utilisé pour décrire le graphique de certaines relations ou
fonctions ou un élément d'une figure géométrique quelconque.
couronne,
Surface comprise entre deux cercles coplanaires et concentriques.
crible d'Ératosthène,
Algorithme qui permet de trouver les nombres premiers inférieurs à un nombre donné.
Cet algorithme est décrit par la suite d'instructions ci-dessous:
Pour trouver tous les nombres premiers jusqu'à un nombre n donné:
écrire dans un tableau la liste de tous les nombres naturels jusqu'à n
éliminer 1
marquer 2 et éliminer tous les multiples de 2
faire de même avec 3
choisir le plus petit nombre non souligné et non éliminé (ici 5)
éliminer tous ses multiples
réitérer le procédé jusqu'à la partie entière de la racine carrée de n
Les nombres marqués sont les nombres premiers jusqu'à n.
critère,
n Synonyme de caractère.
croissance, .n.
Notion associée à divers objets mathématiques tels que les suites de
nombres, les fonctions ou des graphiques et qui décrit de quelle façon
un objet augmente (croît) ou diminue (décroît).
croissance linéaire, caractéristique d'un phénomène qui croît de
façon continue, dans un intervalle donné, suivant une règle linéaire ou
de variation directe.
croissance exponentielle
Caractéristique d'un phénomène qui croît de façon continue, dans un
intervalle donné suivant une règle exponentielle.
croissance logarithmique
Caractéristique d'un phénomène qui croît de façon continue, dans un
intervalle donné suivant une règle logarithmique.
croissant, n. Du plus petit au plus grand.
cryptarithme, n,
Jeu dans lequel les chiffres sont remplacés par des lettres ou d'autres symboles dans une opération arithmétique.
Exemple
Remplacer les lettres par des chiffres afin que les nombres obtenus produisent une addition juste :
NEUF
+ UN
+ UN
ONZE
Solution :
1 9 8 7
+ 8 1
+ 8 1
2 1 4 9
cube,
cube d'un nombre
Produit de trois facteurs égaux à ce nombre.
cube géométrique. Le cube géométrique
Polyèdre régulier dont les six faces sont des carrés.
Histoire
Le terme cube désignait à l'origine un dé à six faces, de ceux que l'on
utilise pour jouer et qui peuvent rouler parce que leurs coins sont
arrondis.
La notation symbolique c³ a été interprétée par les géomètres grecs
comme désignant le volume d'un cube de côté c. Les mathématiciens qui
ont par la suite traduit et adapté les travaux des géomètres grecs ont
conservé cette notation pour désigner la valeur d'une quantité élevée à
la troisième puissance.
C'est ce qui explique pourquoi les termes carré et cube se retrouvent
dans la terminologie utilisée en arithmétique pour décrire certains
nombres.
cube d'un nombre, produit de trois facteurs égaux à ce nombre.
cube géométrique,n. le cube géométrique
Polyèdre régulier dont les six faces sont des carrés.
Histoire.
Le terme cube désignait à l'origine un dé à six faces, de ceux que l'on
utilise pour jouer et qui peuvent rouler parce que leurs coins sont
arrondis.
La notation symbolique c³ a été interprétée par les géomètres grecs
comme désignant le volume d'un cube de côté c. Les mathématiciens qui
ont par la suite traduit et adapté les travaux des géomètres grecs ont
conservé cette notation pour désigner la valeur d'une quantité élevée à
la troisième puissance.
C'est ce qui explique pourquoi les termes carré et cube se retrouvent
dans la terminologie utilisée en arithmétique pour décrire certains
nombres.
Cycle, suite d'éléments d'un phénomène qui se répète de manière continue.
Dans un graphe non orienté, chaîne qui commence et se termine au même sommet.
cycle élémentaire. cycle qui ne passe pas deux fois par le même sommet.
Dans le graphe ci-contre, la chaîne C-D-F-C est un cycle élémentaire.
cycle eulérien, cycle simple qui passe par toutes les arêtes d'un graphe non orienté.
Il n'est pas possible de définir une cycle eulérien dans le graphe de droite.
cycle hamiltonien, cycle qui passe une et une seule fois par chacun des sommets d'un graphe non orienté.
Dans le graphe ci-dessus, la chaîne E-F-D-C-B-A-E est un cycle hamiltonien.
cycle simple
Cycle qui n'utilise pas deux fois la même arête.
Dans le graphe ci-dessus, la chaîne A-B-C-D-E-A est un cycle simple.
cylindre
Solide limité par une surface cylindrique dont la directrice est une
ligne courbe fermée, et par deux plans parallèles entre eux qui ne
contiennent aucune génératrice.
cylindre droit, cylindre dont les génératrices sont perpendiculaires aux bases.
cylindre oblique, cylindre dont les génératrices ne sont pas perpendiculaires aux bases.
cylindre tronqué
Solide obtenu en coupant un cylindre par un plan non parallèle aux bases et qui coupe toutes les génératrices.


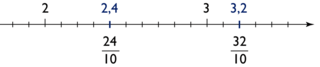
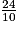 et
et 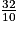 .
.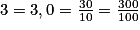 .
.



























