Configurations and Squares by Steven H. Cullinane

4x4 and 3x3

For a definition of "abstract configuration," see Dolgachev— 

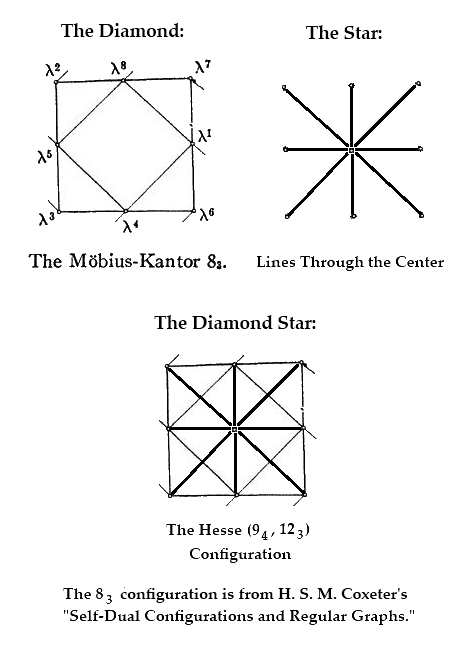
The 3×3 Square

For the Hesse configuration, see (for instance) the passage from Coxeter quoted in Quaternions in an Affine Galois Plane—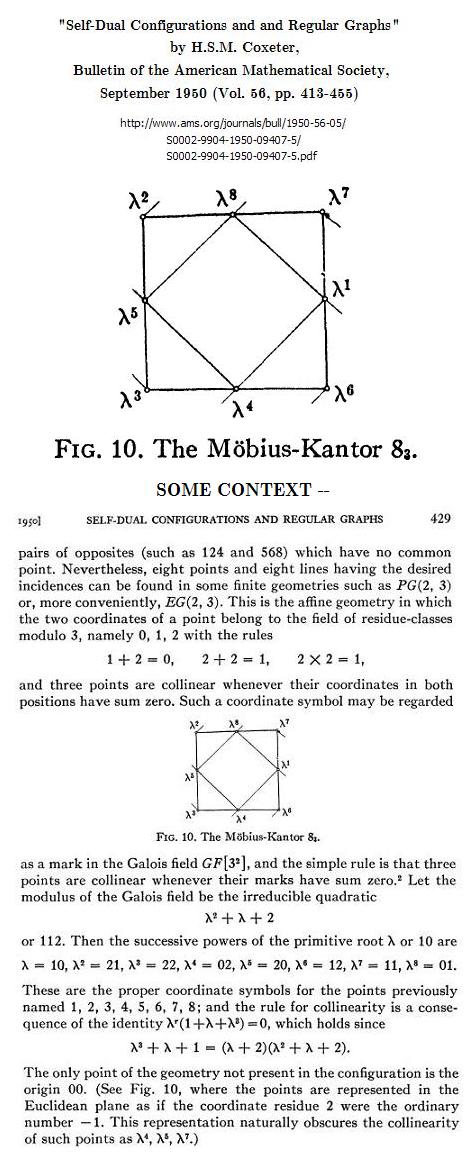

The (8₃, 8₃) Möbius-Kantor configuration here described by Coxeter is of course part of the larger (9₄, 12₃) Hesse configuration. Simply add the center point of the 3×3 Galois affine plane and the four lines (1 horizontal, 1 vertical, 2 diagonal) through the center point.


PART II-- September 7,  2011

The Most Important Configuration

A search for some background on Gian-Carlo Rota's remarks
in Indiscrete Thoughts * on a geometric configuration
leads to the following passages in Hilbert and Cohn-Vossen's
classic Geometry and the Imagination—

These authors describe the Brianchon-Pascal configuration
of 9 points and 9 lines, with 3 points on each line
and 3 lines through each point, as being
"the most important configuration of all geometry."
Thus it seems worthwhile to relate it to the material
on the 3x3 array in Part I above.
The Encyclopaedia of Mathematics , ed. by Michiel Hazewinkel,
supplies a summary of the configuration apparently
derived from Hilbert and Cohn-Vossen—