Mettant en vedette le diamant

"In any geometry satisfying Pappus's Theorem,
the four pairs of opposite points of 8₃ 
are joined by four concurrent lines."
-- H. S. M. Coxeter (see below)
Part II related the the Pappus configuration to the "Diamond Star" figure--

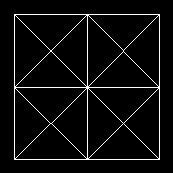
  Stylized version of the
"Diamond Star" in Part I above 

Coxeter, in "Self-Dual Configurations and Regular Graphs," also relates Pappus to this figure.
Some excerpts from Coxeter—

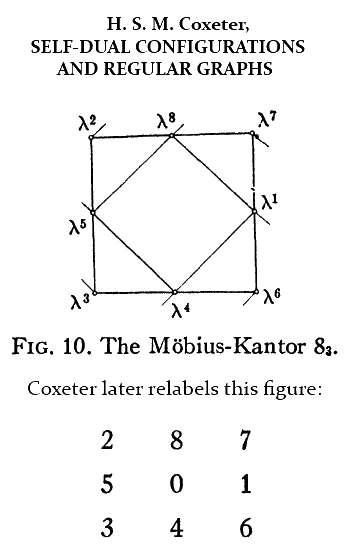
The relabeling uses the 8 superscripts
from the first picture above (plus 0).
The order of the superscripts is from a
Singer 8-cycle in the Galois field GF(9).

The relabeled configuration is used in a discussion of Pappus—

Coxeter here has a note referring to page 335 of  G. A. Miller, H. F. Blichfeldt, and L. E. Dickson, Theory and Applications of Finite Groups, New York, 1916.
Coxeter later uses the the 3×3 array (with center omitted) again to illustrate the Desargues  configuration—

The Desargues configuration is discussed by Gian-Carlo Rota on pp. 145-146 of Indiscrete Thoughts—

"The value  of Desargues' theorem and the reason  why the statement of this theorem has survived through the centuries, while other equally striking geometrical theorems have been forgotten, is in the realization that Desargues' theorem opened a horizon of possibilities  that relate geometry and algebra in unexpected ways."