L’AFRIQUE, BERCEAU DES MATHEMATIQUES

I. SE RE-EDUQUER POSITIVEMENT

L’histoire de l’Afrique et de sa dispora a profondément aliéné la famille africaine qui a renoncé à répondre à sa vocation et a défini sa conscience entièrement par rapport à l’autre, s’interdisant ainsi d’être soi-même. Il s’agit à présent de remplacer un modèle éducatif basé sur la négativité et l’interdit, par un modèle autorisant l’individu à puiser dans ses savoirs ancestraux et à être soi-même.

1. Apprendre grâce aux jeux. Par Quiko Jean-Paul, association GwaJika

Certains jeux et jouets traditionnels sont propices à une forme de contractualisation didactique et aident à acquérir une meilleure compréhension du contexte traditionnel. La roue permet de comprendre ce qu’est le cercle, le cerf-volant le losange, la marelle les chiffres, … La manière de jouer aide à compter et à assimiler l’utilisation de l’espace. Les jeux traditionnels s’inscrivent dans le contexte culturel des élèves et ainsi les erreurs de représentation de la notion sont réduites. Ils saisissent mieux l’importance des notions géométriques.

L’objectif de l’ensemble de la géométrie du CE2 au CM2 est de passer d’une reconnaissance perceptrice des objets à une étude fondée sur le recours aux instruments de tracé et mesure (compas, équerre, …). On peut retrouver les figures géométriques dans la toupie, le cerf-volant … Les élèves comprennent ainsi mieux les relations et propriétés géométriques comme l’alignement, la perpendicularité, … L’usage des jeux traditionnels à travers les mathématiques allie l’aspect théorique à l’aspect pratique des notions enseignées. Le programme entier de mathématiques peut être mis en œuvre sous forme de projets autour de jeux : le jeu de pichin introduit à la notion d’ensemble et au calcul des sommes et des différences, la marel aux chiffres et à la maîtrise de l’espace, … les échasses aux cylindres et volumes, …

L’enseignement des maths à travers les jeux traditionnels revêt de nombreux avantages pour les apprenants et les enseignants. L’apprentissage se fait de façon ludique, dans une atmosphère de détente. De plus, ceux qui ont des aptitudes manuelles sont valorisés. C’est l’avantage d’utiliser des jeux traditionnels pour faciliter et acquérir des notions, des savoir faire, et des compétences dans différentes disciplines. Cela aide à stimuler les jeunes en positivant le savoir mathématique, dans une démarche de proximité.

2. Education et effet Pygmalion. Par Akwa Ekima, psychologue en milieu éducatif.

Il y a un lien entre l’effet Pygmalion, l’estime de soi et la confiance en soi. Dans la mythologie grecque, Ion, fils de Bélos, s’éprend d’Aphrodite qui ne voulait pas lui céder. Il fit une statue en ivoire et la coucha dans son lit. Aphrodite pénétra dans cette statue. Ce mythe sert à montrer que nos croyances ont tendance à se réaliser.

En 1948, Robert Merton forge, à partir de l’effet Pygmalion, le concept de prophétie auto-réalisatrice. Ce concept explique, par exemple, le fait que les prévisions des actionnaires sur la bourse finissent par se concrétiser et faire que le marché s’écroule et provoque un crash.

Rosenthal fait une expérience similaire sur des rats. Il partage le groupe de rats sur lequel il travaille en deux groupes et dit à ses étudiants que le premier groupe de rats est constitué de bons rats et le second groupe de mauvais rats. Les étudiants, persuadés d’avoir affaire à des rats intelligents, sont patients avec ceux du premier groupe et obtiennent de bons résultats avec eux, ce qui n’est pas le cas avec le deuxième groupe.

Rosenthal applique le même principe aux élèves. Si, dès le début de l’année, on désigne au maître, les élèves soit disant doués, la croyance du maître se vérifiera. Les enfants issus de classes sociales défavorisées auront de mauvais résultats, conformément aux attentes du professeur à leur égard.

David Trouillot a observé le comportement des instituteurs dans les ghettos américains. Le destin de certains est scellé dès les 8 premiers jours d’école maternelle, l’instituteur ayant repéré les éléments « rapides » et les éléments « lents ». Les plus « rapides » sont vite placés au premier rang de la classe, et l’instituteur leur consacre l’essentiel de son temps et de son énergie. Cette discrimination ne tarde pas à provoquer une agitation dans les rangs les plus éloignés, que le maître va réprimander sans discontinuer, entraînant des résultats de moins en moins bons de la part de ces élèves, conformes aux attentes originelles de l’enseignant. La dévalorisation des élèves « lents » par l’instituteur a été perçue par les enfants qui ont intériorisé l’image à laquelle l’enseignant les a assignés. Les labels « rapides » et « lents » assignés par l’enseignant se sont cristallisés, au cours de l’année, en bons et mauvais résultats.

Marshall Rosenberg a confirmé la thèse des prophéties auto-réalisatrices en énonçant : « la puissance des prophéties auto-réalisatrices s’applique aussi en éducation ; pour transformer un mauvais élève en bon élève, comportez-vous comme s’il était bon ».

Audrey Akoun et Isabelle Pailleau ont appuyé la thèse de la prophétie auto-réalisatrice en démontant le mythe selon lequel « On n’a rien sans effort ». Les préjugés et attentes ont un impact puissant sur les résultats obtenus par les individus. Lorsque les personnes sentent qu’on leur fait confiance et qu’on attend des résultats d’eux, elles réussissent mieux.

Martin Seligman a travaillé sur la résignation des sujets. Il a démontré qu’un animal finit par se résigner aux chocs électriques. Il extrapole ce résultat aux élèves qui se convainquent qu’ils ne sont pas capables d’apprendre. En effet, c’est à force d’entendre qu’il n’est bon à rien que l’enfant finit par ne plus travailler et faire des efforts.

Les comportements négatifs et positifs s’auto-renforcent avec les étiquettes que l’on colle aux individus.

L’effet Placebo est la tendance à la résolution auto-réalisatrice des prédictions. Si vous pensez que vos enfants ont des ressources, ils vont vous donner raison. Ce qu’on attend de quelqu’un se réalise.

Les travaux menés montrent qu’il est possible de modeler une personne selon les résultats qu’on attend d’elle. Ces attentes sont d’autant plus efficaces qu’elles viennent de l’encadrant (professeur, parent, …). Rien n’incite plus un enfant à donner la bonne, qu’une parole d’encouragement comme « Vas-y, je sais que tu connais la réponse ».

3. Tendre vers une éducation positive. Par Kimya Shomari.

L’effet Pygmalion interroge notre sens aux croyances. Nous avons des représentations et attitudes dépréciatives envers nous et nos enfants. Nous avons des difficultés à gérer nos émotions et notre colère. Nous avons des difficultés à nous faire confiance pour oeuvrer à un objectif commun.

L’esclavage a constitué une rupture brutale avec la matrice culturelle africaine sur le plan physique, psychologique, culturel, social (destruction des liens) et sociétal (violence institutionnalisée, hiérarchisation raciale). Le processus de déshumanisation lié au préjugé de couleur a désintégré les sujets. La peur de déplaire au maître et la conformité à l’extériorité ont aggravé la déshumanisation.

Les notions négatives et haineuses (« le noir, bien meuble », ….) ont été intégrées.

Le style autoritaire de la famille vient prolonger les fonctionnements négatifs mis en place par l’histoire. Les parents préconisent l’obéissance et le respect des règles familiales et accordent peu de place aux dimensions affectives et relationnelles. Ils recourent peu au dialogue, les enfant devant se plier aux règles qu’on leur impose. Le contrôle psychologique et le contrôle comportemental détruisent le libre arbitre. Le modèle éducatif est basé sur l’interdit et la négativité. Il bride la créativité des enfants, leur donne enfants une perception pessimiste de l’existence, et compromet leur capacité à exprimer de façon saine leurs émotions, en raison des qualités relationnelles insuffisamment développées.

Aujourd’hui, il s’agit de se reconstruire, en se reconnectant à notre vision africaine du monde. La reconnaissance et la reconstruction font partie du cycle de changement que nous voyons dans la nature.

Kimia Shomari

Nous sommes à la fois émetteurs et récepteurs des vibrations (pensées, paroles, actions, …) positives ou négatives, de ces rythmes si importants pour nos ancêtres. Il nous faut retrouver la positivité et la substituer à la négativité qui nous habite et dont le but est de détruire les fondements de l’harmonie intérieure de l’individu de façon permanente.

Il nous faut retrouver notre authenticité et la pratique de la justesse, ces valeurs étant incarnées dans la Maât, principe de justice, de vérité et d’harmonie. La justesse est une démarche intérieure visant à être le plus ajusté possible avec la loi fondamentale de l’harmonie. Il n’y a pas de séparation entre le monde visible et le monde invisible. Observer les animaux nous aide à réaliser cet ajustement.

Il nous faut adopter une nouvelle perception de ce qu’est être un être humain. Être humain, c’est révéler ses qualités divines et être capable de réussir son projet de vie. C’est éduquer nos enfants avec de la positivité et une guidance plus juste. C’est les aider à acquérir un esprit scientifique, c’est-à-dire les aider à aimer les faits. Plutôt que de leur apporter des réponses toutes faites, il faut les laisser exercer leur jugement et solliciter leurs connaissances intuitives. Il faut les encourager à aimer la découverte via les voyages, les lectures, … Il faut inculquer l’art d’être responsable et la maîtrise de soi. Pour cela, leurs parents doivent leur donner l’exemple par leurs paroles et par leurs actes. Il leur faut montrer les nuances positives du créole, celles qui servent à refléter la douceur en nous.

Il faut puiser dans nos savoirs ancestraux pour effacer dans nos consciences toute trace des traumatismes laissés par l’histoire. Il faut mettre dehors l’étranger qui est en nous et redevenir souverain de nos royaumes intérieurs.

4. Le droit de se tromper. Par Claire Rondel (Ted Lyon), chef d’entreprise.
   Claire Rondel interpelle sur l’éducation positive. Le cabinet GEM a conduit une étude montrant que 6 % des adultes créent une entreprise en France, plaçant notre pays 56è sur les 59 pays étudiés. Ceci s’explique par le fait qu’en France, l’éducation nous inculque immense peur de l’échec. Cela nous vient de notre éducation dont une règle apprise et ancrée est qu’il est interdit de se tromper, et que si on se trompe c’est parce que on ne maîtrise pas son sujet ou qu’on n’a pas assez été attentif.

Alors qu’en Asie, apprendre est une source de plaisir, en France, l’enthousiasme des enfants par rapport à l’école est diminué par des considérations telles que « Je suis fatiguée d’avoir peur de me tromper ». Le règle française est : «  il est interdit de se tromper ». Cela a quatre conséquence s:

• l’intolérance. Nous devons enseigner à nos enfants qu’il y a autant de codes que de cultures et qu’aucun code ne doit prévaloir sur l’autre.
• mauvaise estime de soi. A force de s’acharner sur ses échecs et ses mauvaises notes, l’enfant finit par se convaincre qu’il est nul. Au lieu de se focaliser sur les erreurs et faiblesses de l’enfant, il faut se focaliser sur ses forces.
• manque d’autonomie face à l’erreur. Dans les usines japonaises, au lieu de mettre un contrôleur en bout de chaîne, c’est chaque opérateur qui, à son poste, détecte l’erreur. Aujourd’hui, on met derrière chaque enfant, un adulte (enseignant, parent, ..). Il en résulte que l’enfant cherche à faire plaisir à l’adulte et veut éviter de se faire réprimander par l’adulte. Il faut plutôt apprendre à nos enfants à être autonomes et à détecter leurs erreurs tout seuls.
• manque de persévérance. Churchill disait : « Le succès, c’est d’aller d’échec en échec sans perdre son enthousiasme ». Si on interdit aux enfants de se tromper, ils n’apprendront jamais à réussir.
  Les enfants d’aujourd’hui sont la société de demain. Il faut changer notre message et entrer dans une nouvelle ère, de fin d’interdiction, une ère où nous allons accorder à nos enfants le droit à l’erreur.

5. Le danger de l’histoire unique. Par Shimaia Mandja Atchi.

Shimaia Mandja Atchi (Nigéria)

Toute petite, au Nigeria, Shimaia Mandja Atchi lisait des livres anglais et américains. Elle commence à écrire à l’âge de 7 ans. Les histoires qu’elle écrit sont comme celles qu’elle lisait, à savoir des histoires avec des personnages blancs aux yeux bleux, et cela malgré que qu’elle vivait et grandissait au cœur de l’Afrique Noire, au Nigeria. Ses histoires parlent de neige, de pommes, de ginger beer, … alors que rien de cela n’existait au Nigeria. La famille emploie comme domestique une jeune femme nommée Fidé. Shimaia est pleine de pitié condescendante pour cette domestique issue d’un village très pauvre. Un jour que Shimaia rend visite à Fidé, elle découvre que les habitants de ce village ne sont pas seulement des « pauvres » mais aussi des hommes et des femmes vivant de belles valeurs comme l’amour du travail, la solidarité, le sens de l’accueil, … et qu’ils produisent de très beaux travaux d’artisanat.

Tout change quand elle découvre les romans de Chinua Achebe et Camara Laye. Cela l’aide à ne plus avoir une vision unique de l’Afrique et du monde. Elle commence à guérir de cette vision unique et négative qu’ont inventée John Locke, avec son « Histoire unique de l’Afrique » écrite en 1651, et la génération d’auteurs coloniaux qui ont sévi pendant plusieurs siècles. Selon eux, l’authenticité africaine n’était faite que de pauvreté et de malheurs. Selon leurs critères, les personnages que Shimaia commençait à dépeindre dans ses romans n’étaient pas authentiquement africains car ils n’étaient pas affamés et conduisaient des voitures.

Lorsque Shimaia arrive aux Etats-Unis pour y poursuivre ses études aux USA. Sa compagne de chambre universitaire lui demande à écouter des extraits de sa musique « tribale ». Elle a « pitié » de Shimaia, « pauvre » africaine. Sa compagne montre ainsi qu’elle avait une « histoire unique » de l’Afrique, histoire faite de catastrophe et de misérabilisme. Pour l’américaine, l’Afrique a de beaux paysages mais ses habitants sont des miséreux qui attendent d’être sauvés par les blancs. Dans ces conditions, aucune possibilité de rapport égalitaire entre les deux étudiantes, entre l’américaine et Shimaia l’africaine, n’est possible.

Nkali s’intéresse à la notion d’« être plus grand que l’autre ». Celui qui raconte les histoires et comment il les raconte sont souvent liés au désir d’être plus grand que l’autre. Le palestinien Mourid affirme : «  Si vous voulez déposséder les autres, racontez leur histoire ». Commencer par l’échec d’un pays africain et non par sa création coloniale biaise le récit qu’on va faire.

L’histoire unique crée des stéréotypes qui, forcément incomplets, font une histoire unique. L’histoire unique vole aux personnes leur dignité. A partir du moment où c’est un africain, Chinua Achebe, qui décide de parler de l’Afrique, les histoires racontées ont été plus équilibrées. De même, le Nigéria raconté par des nigérians parle de Nollywood, des entrepreneurs, la ténacité des nigérians qui essaient, malgré obstacles, … Les histoires ont été utiles pour déposséder les gens de leur dignité et les vaincre. Heureusement, ceux-ci ont la possibilité de se reconstruire en racontant leur propre histoire. C’est ce qu’a fait Chinua Achebe.

III. LES MATHEMATIQUES AFRICAINES

1. Les mathématiques africaines : traditions culturelles et modernité technologique.

Pour bâtir la paix de demain, il nous faut chérir la paix en nous. Pour cela, l’estime de soi est essentielle. S’estimer soi, se faire confiance, s’aimer, ne pas se dévaloriser est essentiel pour bien vivre sa vie et bien vivre avec les autres.

L’article 26 de la déclaration universelle des droits de l’homme précise que « l’éducation doit viser au plein épanouissement de la personnalité humaine «

L’Histoire Générale de l’Unesco a quant à elle pour objectifs de : « désarmer l’histoire en mettant l’accent sur le développement scientifique et culturel et en soulignant les apports de tous les peuples au progrès général de l’humanité ; écrire une histoire de l’humanité reflétant la pluralité des visions, souligner les interactions entre les cultures et mettre en évidence les valeurs partagées qui en découlent ; construire des ponts entre les cultures et promouvoir le respect mutuel ; constituer un corpus de connaissances disponible pour des déclinaisons de tous ordres ». Concernant l’Afrique, il s’agit de : « décoloniser l’histoire africaine et montrer la diversité des idées, des cultures, des sociétés et des institutions du continent ; mettre en lumière les origines africaines de la civilisation égyptienne, la formation des grandes entités politiques et socioculturelles du continent et les relations de l’Afrique avec le reste du monde et la diaspora ; créer une nouvelle vision de l’Afrique, dépassant les divisions coloniales et éloignée de la perception raciste ; mettre en lumière les liens entre les Africains d’une part et entre l’Afrique et le reste du monde d’autre part ».

2. Lutter contre la dévalorisation de l’autre

Les manuels scolaires regorgent de stéréotypes de dévalorisation de l’autre et, partant, de discrimination. Il s’agit en particulier des stéréotypes contre les femmes, les noirs, la pauvreté, …

La Halde indique que la lutte contre l’exclusion des minorités visibles passe d’abord par l’introduction des minorités visibles dans les manuels et par la valorisation de leurs auteurs, de leurs personnages, de leurs contextes, … Il faut ensuite éviter l’utilisation des stéréotypes dans la représentation des minorités visibles et éliminer les représentations ségrégationnistes, négatives et choquantes. Pour beaucoup de français, noir est encore synonyme d’esclave. Leur subconscient reste imprégné de personnages comme Candide, noir et donc esclave. Il faut relativiser l’adage « Je pense donc je suis », car bien souvent nous croyons penser alors que nous ne faisons que penser ce que la société nous conduit à penser. Penser est une chose très difficile car cela suppose tout un travail pour nous libérer de tous les conditionnements qui nous empêche d’accéder à la vérité des choses. De nombreux ouvrages (par exemple, « Le grand livre de l’histoire du monde ») sont particulièrement nocifs pour les enfants car ils enferment leur intelligence dans des stéréotypes.

L’année 2014 est l’année des mathématiques, au carrefour des cultures. Cette année veut mettre en lumière l’histoire de mathématiques dans toutes les traditions (Occident, monde arable, indien, chinois) et leur lien avec l’art.

Jean-Philippe Omotundé

L’approche « scientifique » est, elle aussi, très souvent pernicieuse. Ainsi, parlant de la paléoanthropologie, Pascal Picq affirme : « L’odyssée de l’espèce humaine est un ramassis de mythes de l’exclusion basés sur la domination de l’homme occidental blanc ».

Pourtant, la découverte des cranes Omo I et II en 1967 par Richard Leakey a confirmé l’origine africaine de l’homme.

Dans le domaine de l’art, la primauté africaine est également établie. Le premier corpus artistique qu’est le kouros n’est pas européen. Les kouros grecs (jumeaux de Delphes de – 530, le kouros en marbre de – 520) trouvent leur origine dans le kouros de l’Afrique antique (Ramses II de – 1 300, Menkaouré de – 2700, Chansou – 2 700, …). Les Grecs ont appris à sculpter en Afrique.

3. L’homo sapiens est né en Afrique
   Jusqu’en 2002, les chercheurs occidentaux étaient convaincus que la révolution culturelle des Homo Sapiens avait eu lieu en – 35 000, lors de leur installation en Europe. Ils se basaient pour cela sur les peintures de la grotte de Chauvet (Ardèche), découverte en 1994. Le site comporte un millier de peintures et de gravures, datant de – 30 000 ans. Avec Lascaux (découverte en 1940), Cosquer (découverte en 1991) et Cussac (découverte en 2000), la grotte Chauvet est l’une des grottes françaises majeures par les qualités esthétiques et le nombre de ses œuvres. Elles sont souvent considérées comme les « premiers chefs d’oeuvre de l’humanité ».

Pinnacle Point

Or, près de Mossey Bay, en Afrique du Sud, on a découvert Pinnacle Point, un complexe de sites préhistoriques datant de – 170 000 à – 40 000 ans. Le site de Pinnacle Point a livré les plus anciennes preuves d’une utilisation contrôlée de la chauffe pour améliorer l’aptitude à la taille des roches utilisées pour fabriquer des outils. Les restes humains découverts datent d’environ 100 000 ans. Grâce à Pinnacle Point, les paléoanthropologues s’accordent aujourd’hui pour dire que les preuves génétiques et fossiles sont suffisantes pour considérer qu’Homo sapiens est apparu en Afrique il y a environ 200 000 ans.

Blombos

Un peu à l’ouest de Pinnacle Point, à 300 km à l’est de la ville du Cap, on a découvert la grotte de Blombos, avec des blocs d’ocre gravés, perles en coquillage, outils en os, … de plus de 70 000 ans. Les peintures corporelles font des utilisations très complexes de l’ocre. Ces découvertes contredisent l’hypothèse selon laquelle la modernité comportementale n’aurait que 40 000 ans et résulterait d’un grand bon culturel qui aurait eu lieu en Europe. Les outils très raffinés découverts à Blombos sont propres à l’Homme anatomiquement moderne, l’Homo sapiens. Blombos est l’exemple de l’inventivité très précoce née en Afrique.

Pierre de Blombos

A Blombos, Christopher Henshilwood a mis en évidence des concepts de triangulation gravés dans la pierre. Sally McBrearty et Alison Brooks ont montré que presque toutes les innovations culturelles sont nées en Afrique. Les éléments de la révolution culturelle humaine sont apparus en Afrique avant d’être exportés vers les autres continents.

Sibudu

La technique consistant à chauffer la pierre avant de la tailler, l’invention de la colle composite (- 68 000 ans), l’invention des lits pesticides (- 77 000 ans), … sont nées en Afrique. Une équipe internationale dirigée par Lyn Wadley, de l’Université de Witwatersrand, à Johannesburg, a découvert, dans le site de Sibudu, en Afrique du Sud, des restes de literie vieux de 38 000 à 77 000 ans, associés à l’utilisation de plantes insecticides.

Diepkloof

Des chercheurs du CNRS ont découvert, dans l’abri sous-roche de Diepkloof, à 180 kilomètres au nord-ouest du Cap, des morceaux de coquilles d’oeuf d’autruche, sur lesquels sont gravés des dessins géométriques. Datant de 60 000 ans, ce ne sont pas les plus anciens dessins, car des morceaux d’ocre gravé datés d’environ 75 000 ans avaient été découverts un peu plus au sud du pays, dans la grotte de Blombos. À Diepkloof, on une tradition graphique manifeste, avec 270 morceaux de coquilles gravées de motifs, qui persistent pendant quelques milliers d’années. Il y en a probablement beaucoup plus, car seule une petite fraction du site a été fouillée. Plus les coquilles sont récentes, plus les motifs semblent diversifiés : réseaux de lignes parallèles se croisant à angle droit, lignes convergeant avec un angle très aigu, etc. Ces pratiques rappellent celles des chasseurs-cueilleurs Bochimans du désert du Kalahari, dont les ancêtres étaient probablement présents dans la région il y a plusieurs dizaines de milliers d’années. Jusqu’à récemment, ces derniers perçaient des oeufs d’autruche pour en consommer le contenu. Puis ils utilisaient les coquilles comme réserve d’eau fermées par un bouchon végétal et enfouies dans des caches. Ces coquilles étaient marquées par des dessins qui en identifiaient le propriétaire et le groupe auquel il appartenait.

5. Os de Lebombo
Un péroné de babouin datant de – 35 000 avant JC a été découvert dans les montagnes du Lebombo entre l’Afrique du sud et le Swaziland, durant les années 70. Le célèbre « Os de Lebombo » possède 29 encoches faites volontairement par l’homme et qui présentent d’étroites similitudes avec les bâtonnets servant de calendrier encore utilisés par les Bushmen de Namibie.
Cet os témoigne de l’existence d’un système de comptage très sophistiqué qui permettait à l’homme de maîtriser le temps (phases de la lune…). C’est la première trace visible de l’émergence de calculs dans l’histoire de l’humanité, comme en témoigne le chercheur anglo-saxon Richard Mankiewicz : « Le plus ancien témoignage de calcul numérique a été exhumé au Swaziland en Afrique Australe. Il date d’environ 35 000 ans av. J. C. et consiste en un péroné de babouin portant 29 encoches nettement visibles ».

6. Os d’Ishango
L’os d’Ishango est un os de babouin datant du paléolithique (- 20 000 ans) et découvert en 1950 par l’archéologue belge Jean de Heinzelin de Braucourt, à Ishango, sur les rives du lac Edward, à la frontière entre la République Démocratique du Congo et l’Ouganda, dans le Parc des Virunga. L’os est aujourd’hui exposé au Muséum des Sciences naturelles à Bruxelles. Il mesure 10 cm environ.

7. L’os présente 168 entailles réparties en 16 groupes, alignés sur trois colonnes. Les groupes d’entailles représentent des nombres naturels. Les entiers naturels sont notés dans un système unitaire. L’entier naturel 5 correspond à un groupe de 5 entailles. Aujourd’hui, ce système de numération est toujours utile, par exemple pour noter les scores dans un sport.

Os d’Ishango

De manière certaine, l’os d’Ishango démontre que l’homme savait compter au Paléolithique, bien avant l’apparition de l’écriture. L’os d’Ishango démontre que les Bantous maîtrisaient dès cette époque les suites arithmétiques, les duplications, les multiplications, les soustractions et connaissaient même les nombres premiers.
Une statue de 7 m de haut, représentant l’os d’Ishango, a été dressée à Bruxelles et témoigne que la première tablette de calcul a été trouvée en RDC.
Il est possible que, passant de l’Afrique Centrale à l’Egypte Antique puis à la Grèce, le système numérique de l’os d’Ishango soit une de ses plus grandes dettes que le monde moderne doit à l’Afrique Noire. Que ce soit le cas ou non, il reste remarquable que l’indication la plus ancienne de l’utilisation d’un système numérique par l’homme date du paléolithique en Afrique Centrale. Aucune fouille en Europe n’a révélé un tel indice.
On peut confondre les marques de l’os d’Ishango « IIIII » avec un code barre. C’est une confusion heureuse. Les mathématiques semblent avoir commencé avec des traits et retrouvent  actuellement leur expression initiale dans les codes du supermarché. Si l’Amérique a reconnu la contribution des afro-américains dans l’édification de sa culture et de sa civilisation, l’Europe semble avoir besoin de beaucoup plus de temps pour reconnaître l’apport des africains dans le développement des sciences.
Selon Le Monde du 28 février 2007, « les os incisés d’Ishango font naître la numération en Afrique. Il s’agit du plus ancien témoignage des capacités mathématiques de l’humanité ».

7. Fractales africaines
Ron Eglash, cybernéticien américain de l’University of Ohio a établi que beaucoup de traditions culturelles africaines sont fondées sur des algorithmes ou sur des mathématiques. Ces algorithmes sont les fondements de notre modernité technologique.

Georg Cantor
Ron Eglah explique qu’en Allemagne, en 1877, un mathématicien nommé Georg Cantor. Cantor décide de prendre une ligne, d’en effacer un tiers au milieu, de prendre les deux lignes restantes et de leur appliquer le même processus, un processus récursif. Il commence donc avec une ligne, et puis deux, et puis quatre, et ensuite 16, et ainsi de suite. Et s’il le fait un nombre infini de fois, ce que l’on peut faire en mathématiques, il obtient un nombre infini de lignes, chacune étant constituée d’un nombre infini de points. Il réalisa donc qu’il était face à un ensemble dont le nombre d’éléments était supérieur à l’infini. Il était convaincu qu’il avait été mis sur Terre pour fonder la théorie des ensembles transfinis, parce que le plus grand ensemble de l’infini serait Dieu lui-même. C’était un homme très religieux. C’était un mathématicien avec une mission.

Von Koch

Un mathématicien suédois, von Koch, décide, au lieu de soustraire des lignes, de les ajouter. Il aboutit à une magnifique courbe. Rien n’oblige à commencer par cette forme initiale ; on peut utiliser la forme initiale que l’on souhaite et par itération, la forme initiale se déplie en une structure très différente. Tous ces exemples possèdent la propriété d’autosimilitude : la sous-partie ressemble à l’ensemble. C’est le même motif à différentes échelles.

Mandelbrot

En 1977, Benoît Mandelbrot, un mathématicien français, réalisa que si l’on utilise des images de synthèses associées aux formes qu’il appela des fractales on obtenait les formes de la nature. On obtient les poumons humains, les acacias, les fougères, et toutes sortes de magnifiques formes naturelles. Si on regarde là où se rejoignent notre pouce et notre index, on voit un pli, et puis une ride au sein du pli, et un pli au sein d’une ride. Notre corps est recouvert de fractales. Les mathématiciens qui disaient que ces formes étaient pathologiquement inutiles, respiraient ces mots avec des poumons fractals.

Ba-Ilas (Zambie)

La nature possède cette structure autosimilaire des fractales. La nature utilise des systèmes qui s’auto-organisent. Si on regarde une photo aérienne d’un village africain, on voit des fractales.

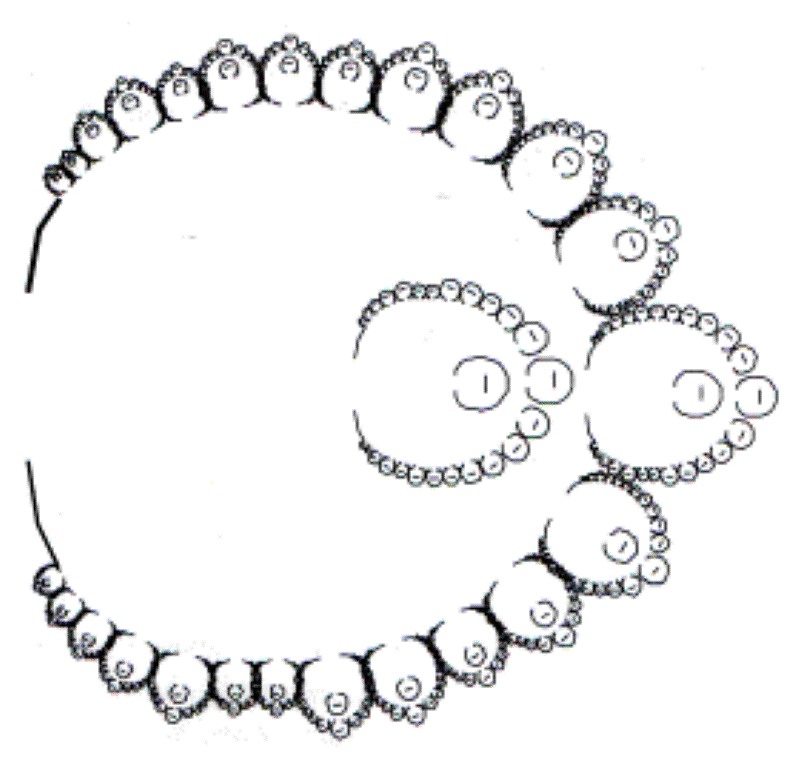
Village Ba-Ila

Dans le sud de la Zambie, les Ba-Ilas ont construit un village d’environ 400 mètres de diamètre. C’est un immense cercle. Les cercles, qui représentent les enceintes familiales, s’agrandissent à mesure qu’on avance vers le fond, puis le cercle du chef à l’arrière et la famille proche du chef dans ce cercle. Tout est construit sur un modèle fractal : la maison avec l’autel sacré, l’enceinte familiale, puis le village en entier. On a un cercle de cercles de cercles. Ce sont les esprits des ancêtres qui ont suscité ces constructions.

Mandara (Cameroun)
Dans les monts Mandara, à Mokoulek au Cameroun, tout le village suit un tracé en spirale, avec une ligne qui s’autoréplique et se transforme en fractale. On a un seul bâtiment carré du village qui est l’autel sacré, où on fait des sacrifices chaque année pour entretenir les cycles annuels de fertilité des champs. Les cycles de fertilité sont comme les cycles récursifs de l’algorithme géométrique qui construit tout le village. La récursion dans certains villages continue jusqu’à de très petites échelles.

Nankani (Mali)
Dans le village nankani au Mali, dans l’enceinte familiale, les récipients dans l’âtre sont empilés récursivement. Les calebasses sont empilées récursivement. La plus petite calebasse est là pour conserver l’âme de la femme. Et quand elle meurt, on organise une cérémonie où on casse la pile appelée le zalanga et son âme s’envole vers l’éternité. Encore une fois, l’infini est important.
Ces motifs fractals sont-ils communs à toutes les architectures indigènes ? Non, seules les architectures africaines sont fractales. Les autres sociétés utilisent des thèmes de conception géométriques différents. Les Amérindiens utilisent une combinaison de symétrie circulaire et de quadruple symétrie.
Les fractales sont autosimilaires, c’est-à-dire qu’elles sont similaires à elles-mêmes, mais ne sont pas forcément similaires aux autres.
Certains se demandent si les fractales ne relèvent pas simplement de l’intuition. Pour eux, elles ne sont pas vraiment un savoir mathématique. Si certaines fractales africaines sont purement de l’intuition, dans certains autres cas, il y a de vrais algorithmes, comme les sculptures mangbetu où on voit une géométrie récursive, ou dans les croix éthiopiennes où on voit ce merveilleux déploiement de la forme.

Tchokwé (Angola)
En Angola, le peuple Tchokwé dessine des lignes dans le sable. C’est un chemin eulérien : il ne faut jamais lever son crayon de la surface et il ne faut pas repasser sur une même ligne. Les locaux le font récursivement, avec un système basé sur l’âge. Les petits enfants apprennent celui-ci, et les plus grands celui-là, à l’initiation suivante, on apprend un nouveau dessin. A chaque itération de cet algorithme, on apprend les itérations du mythe. On apprend le niveau supérieur de savoir.

Awélé
Partout en Afrique, on voit le jeu de plateau appelé « awélé » au Ghana, « mancala » sur la côte est, « bao » au Kenya, « sogo » ailleurs. On voit apparaître spontanément des motifs auto-organisés dans ce jeu. Les gens au Ghana connaissent ces motifs auto-organisés et les utilisent de façon stratégique. C’est un savoir très conscient.

Brise-vents du Sahel
Partout au Sahel, on peut voir des brise-vents avec des fractales. Dans le reste du monde, les clôtures sont toutes cartésiennes, strictement linéaires. En Afrique, il y a des clôtures fractales, aux proportions non linéaires.L’explication est donnée par un paysan du Sahel : « Si je vivais dans la jungle, je n’utiliserais que de longues rangées de paille, parce qu’elles sont rapides à faire et très peu coûteuses. Ça ne prend pas beaucoup de temps, pas beaucoup de paille. Mais le vent et la poussière y passent très facilement. Les rangées serrées tout en haut retiennent vraiment le vent et la poussière. Mais ça prend beaucoup de temps et de paille, puisqu’elles sont très serrées. Nous savons par expérience que plus on s’éloigne du sol, plus le vent souffle fort. » Le paysan africain fait donc une vraie analyse coût-bénéfice. En mesurant les longueurs de paille et en les retranscrivant sur un graphique logarithmique, Ron Eglash a identifié l’exposant et trouvé qu’il correspond presque exactement à l’exposant de la relation entre la vitesse du vent et la hauteur dans le manuel d’ingénierie du vent. Il en a déduit que les paysans sahéliens font une utilisation concrète d’une technologie fractale.

Bamana (Mauritanie)
Un exemple encore plus complexe d’une approche algorithmique n’est pas en géométrie, mais dans un code symbolique, à savoir la divination bamana par le sable. On retrouve le même système de divination partout en Afrique. On le trouve aussi bien sur la côte Est que la côte Ouest, et les symboles sont souvent très bien conservés. Chacun de ces symboles est un mot binaire à quatre bits : on dessine aléatoirement ces lignes dans le sable, et ensuite on les compte ; si le nombre est impair, on fait une marque, et s’il est pair, on en fait deux. Les africains le faisaient très rapidement, en ne dessinant les lignes aléatoires que quatre fois — Je ne comprenais pas comment ils obtenaient les 12 autres symboles. Quand on a un symbole à quatre bits, on l’associe à un autre à côté. Donc pair plus impair donne impair. Impair plus pair donne impair. Pair plus pair donne pair. Impair plus impair donne pair. C’est exactement l’addition modulaire et plus exactement l’addition modulo 2, où les nombres pairs sont remplacés par 0 et les nombres impairs par 1, comme le contrôle de bit de parité dans l’ordinateur. Ensuite on prend ce symbole, et on le remet en jeu c’est donc une diversité autogénératrice de symboles. Les paysans africains utilisent vraiment une sorte de chaos déterministe pour le faire. C’est un code binaire, comme dans les circuit électroniques.

De l’Afrique en Allemagne, via l’Espagne
Au XIIe siècle, Hugo Santalia a introduit l’addition modulaire en Espagne après avoir vu des mystiques musulmans africains la pratiquer. Et elle a fait son entrée chez les alchimistes européens sous le nom de géomancie ou divination par la terre. C’est ainsi que Leibniz, le mathématicien allemand, parle de la géomancie dans sa dissertation appelée « De Combinatoria. » Et il dit : « Au lieu d’utiliser une marque et deux marques, utilisons plutôt un un et un zéro, et nous pouvons compter par puissances de deux. » Des uns et des zéros, c’est le code binaire. George Boole a pris le code binaire de Leibniz et a créé l’algèbre booléen, et John von Neumann a pris l’algèbre booléen et a créé l’ordinateur numérique. Ainsi, chaque circuit électronique (et donc tous les PDA et ordinateurs) a ses racines en Afrique.
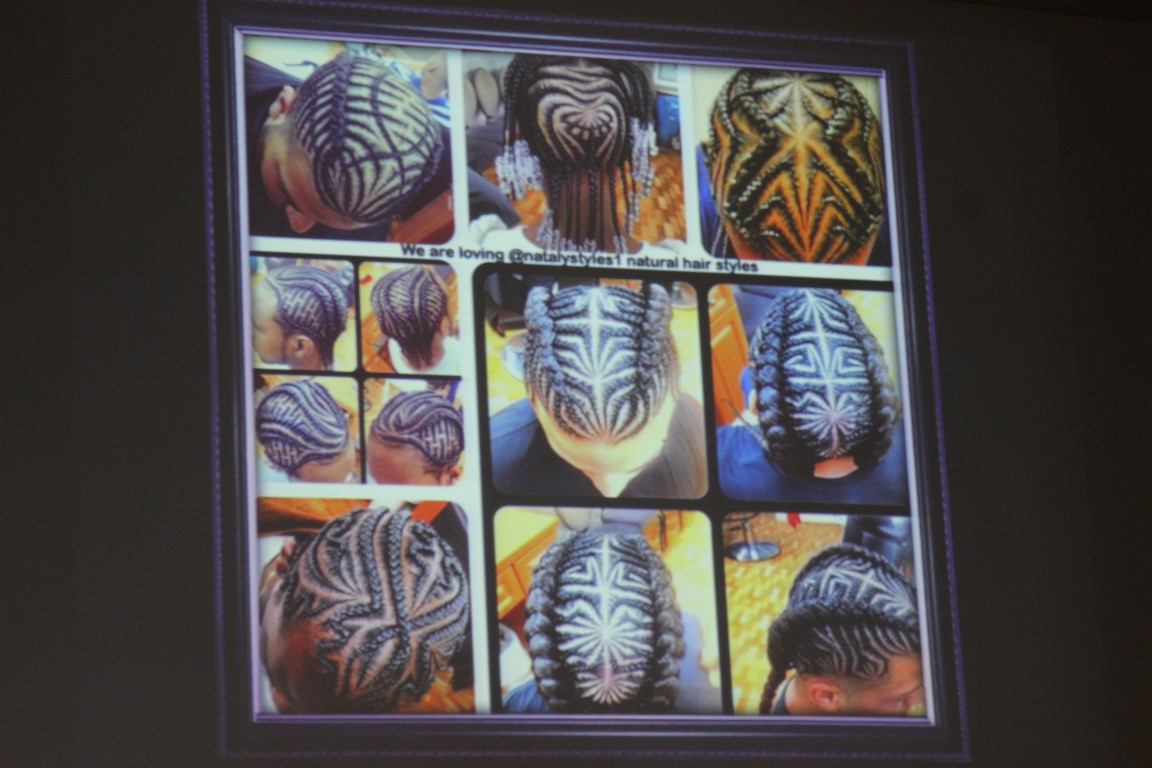
Les fractales s’expriment dans le quotidien des cultures africaines : architecture, coiffures, textile, sculpture, peinture, religion, …

 

5. La numération antique africaine

Multiplier avec des dessins

Pour réaliser des multiplications, les africains utilisaient des traits tracés sur le sol à l’aide d’un bout de bois. Ainsi, pour effectuer la multiplication 15 X 11, le premier nombre (15) est représenté par un premier trait (rouge) pour 1 dizaine et cinq traits parallèles (rouges) pour 5 unités. Le deuxième nombre (11) est représenté par un trait (blanc) pour une dizaine et un autre trait parallèle pour l’unité. On symbolise les intersections par des points (jaunes). On encercle les points en respectant les diagonales. On compte le nombre de points dans chaque cercle et on a le bon résultat de la multiplication, soit 165.

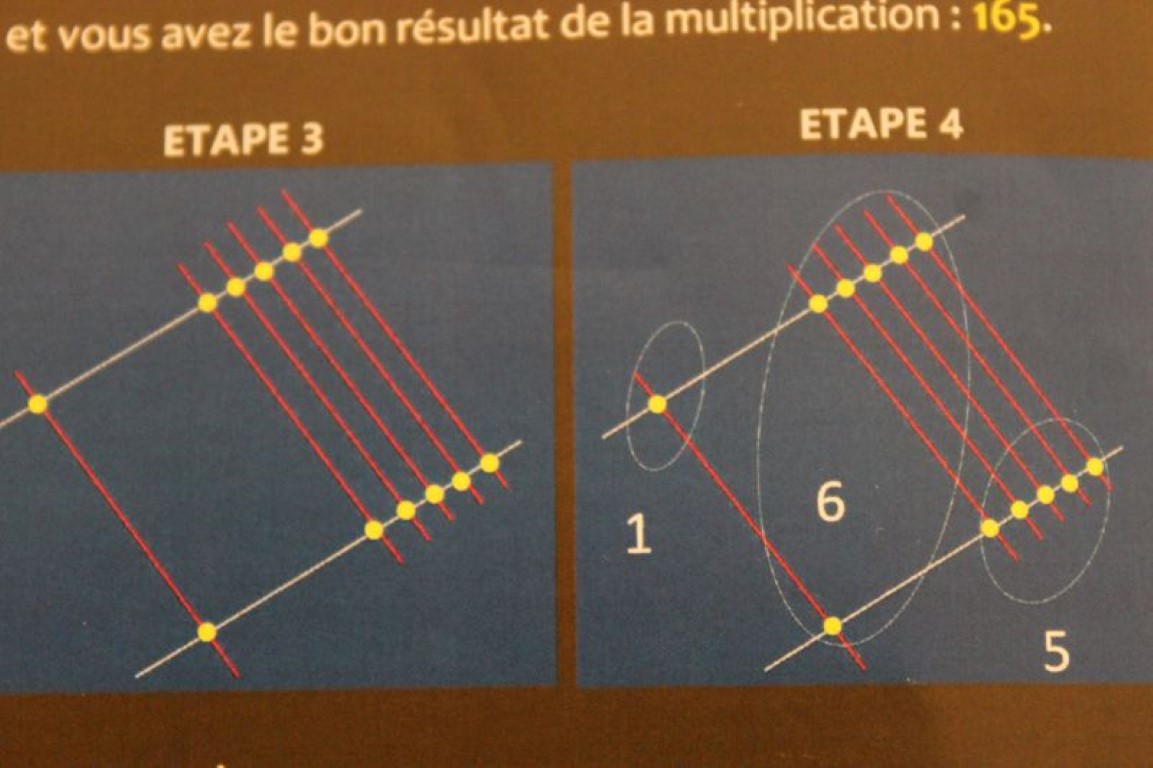
Multiplier avec des traits

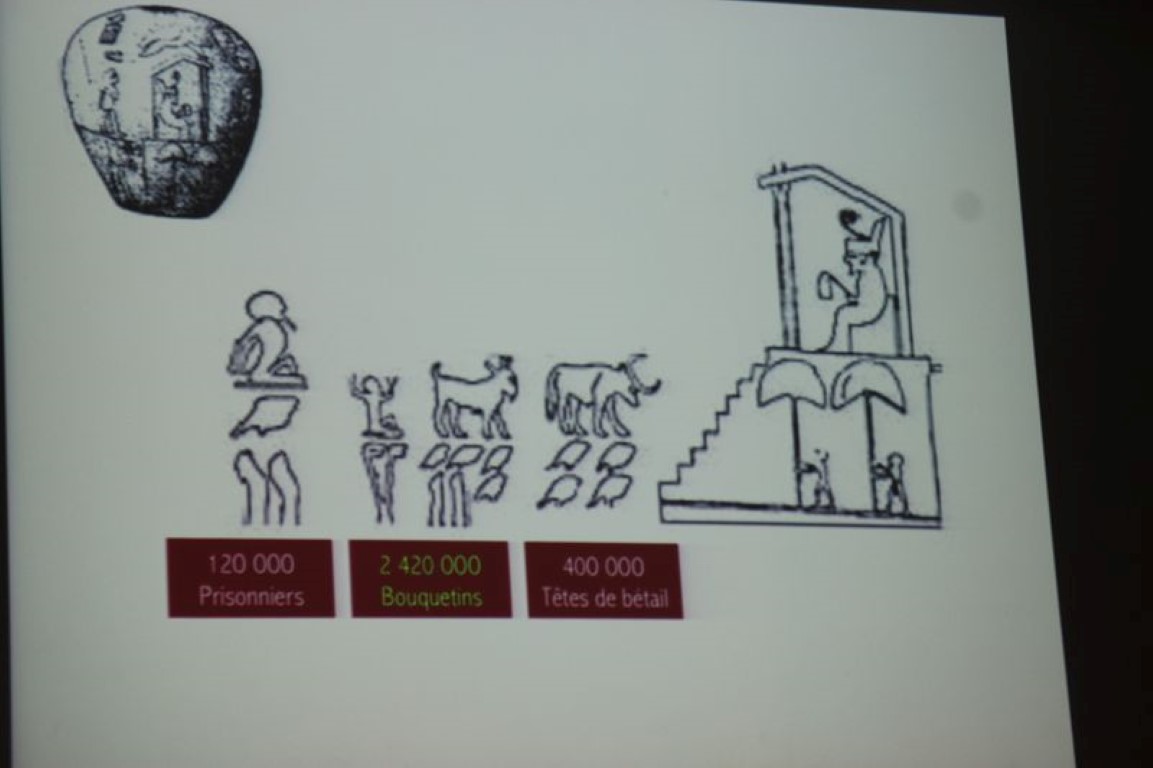
Système égyptien

Au IIIème millénaire avant J.C., en Egypte, les scribes écrivent les nombres sur des papyrus sous forme de hiéroglyphes. Chaque signe possède une valeur qui correspond à l’une des 6 premières puissances de 10. L’unité est une barre verticale ; la dizaine est une anse de panier ; la centaine est une corde enroulée ; le millier est une fleur de lotus ; la dizaine de mille est un doigt dressé ; la centaine de mille est un têtard et le million est le dieu Héhé.

 

Fractions

Nous devons aussi aux Egyptiens de l’antiquité les fractions, puisqu’ils sont à l’origine des fractions de numérateur 1. La mythologie égyptienne raconte que Seth (Dieu de la violence) arrache l’œil à Horus (Dieu à tête de faucon et à corps d’homme) et le partage en 6 morceaux. Chacune des parties de l’œil, appelé Oudjat, symbolise une fraction de numérateur 1 et de dénominateurs 2, 4, 8, 16, 32 et 64. Thot (Dieu humain) reconstitue l’œil, symbole du bien contre le mal mais la somme de ces parts n’est pas égale à 1 (l’œil entier) mais à 63/64. Thot accordera le 64ème manquant à tout scribe recherchant et acceptant sa protection.

Multiplier et diviser en faisant des additions

Ce mode de calcul nous est révélé par deux papyrus : le papyrus de Rindt, rédigé en – 1 650 ans par Ahmès, mathématicien égypto-nubien et qui contient 87 problèmes résolus en algèbre, arithmétique, géométrie et arpentage ; le papyrus de Moscou qui date de – 2000 ans et traite de 25 problèmes mathématiques. Le papyrus de Rindt, lui-même recopié à partir du traité de Yamesu (celui qui a été enfanté par la lune) contient, parmi ses 87 traités de maths, les théorèmes de Thalès et Pythagore. (Ptah-Hour).

Pour effectuer la multiplication 21 X 13, on procède de la façon suivante. Sur la colonne de gauche, on liste les valeurs 1, 2, 3, 4, 5, … Sur la colonne de droite, on pose un des deux termes de la multiplication, par exemple 13, et on l’additionne successivement à elle-même. Ainsi on obtient 13, 26, 39, … Dans la colonne de gauche, on sélectionne les chiffres dont la somme donnera 21, soit 6, 7 et 8. On adygjklnkbjhlkitionne dans la colonne de droite les sommes correspondantes (78 + 91 + 104) et on obtient ainsi le résultat de la multiplication, soit 273.

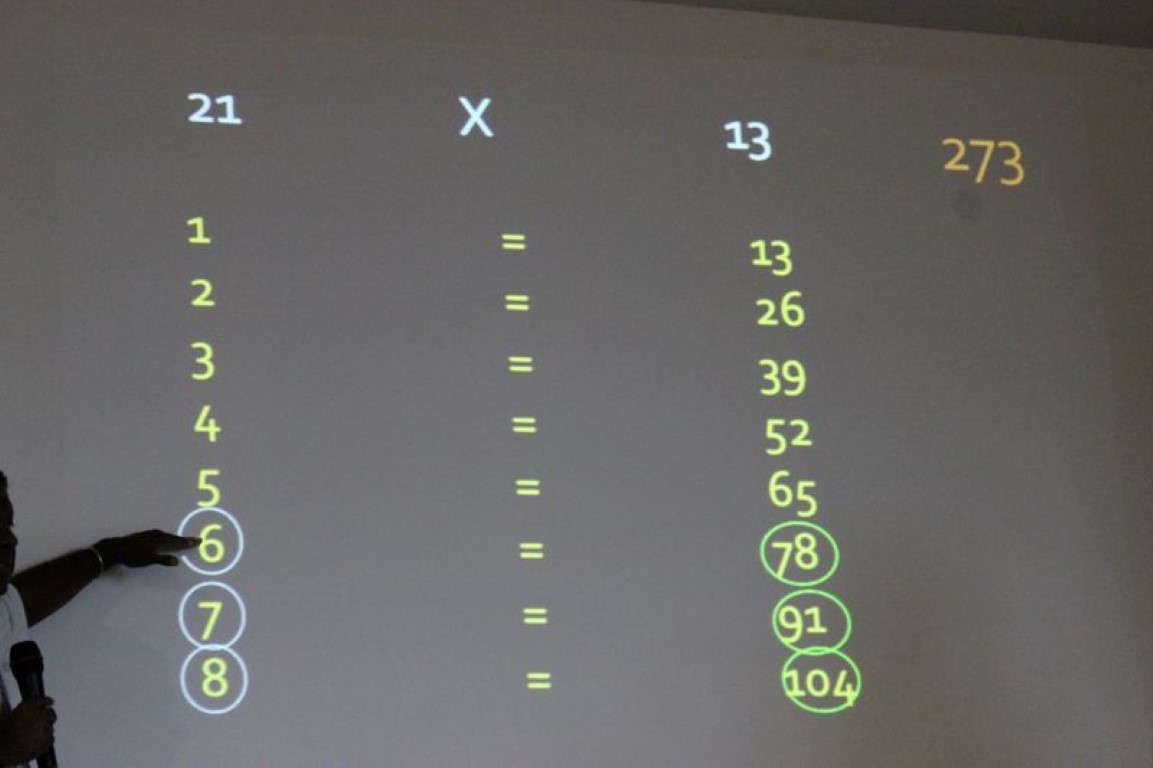
Multiplier avec des additions

Calcul binaire

L’écriture décimale demande 10 symboles (0, 1, 2, 3, 4, 5, 6, 7, 8, 9). Nos 10 doigts en sont à l’origine. Un autre système d’écriture est basé sur deux doigts seulement ? C’est le cas du système binaire (base 2) qui ne dispose que de deux symboles : 0 et 1 (deux doigts!).

Langage binaire africain (Medium)

Le langage binaire se déduit de la méthode de multiplication égypto-nubienne étudiée plus haut. Pour écrire 273, on affecte 1 aux lignes retenues pour la multiplication 21 X 13 et 0 aux autres lignes. 273 s’écrit donc 00000111.

La méthode africaine permet donc de combiner la méthode décimale et la méthode binaire, en retranscrivant le chiffre 273 en 00000111. La programmation des ordinateurs, les circuits électroniques, le code ASCII, … utilisent les nombres binaires pour représenter des symboles tels les caractères, les chiffres, les signes de ponctuation, … Les africains ont donc inventé l’ordinateur numérique bien avant que les temps modernes le découvrent. C’est ce qui pousse Jacques Attali à dire : « Les africains ont inventé une façon de prévoir l’avenir qui est exactement ce qu’on appelle le code binaire ou le code booléen en mathématiques modernes, qui a donné l’ordinateur numérique d’aujourd’hui. Et on sait comment cela s’est transmis : c’est passé de l’Afrique de l’Ouest au 10è siècle par les marchands arabes jusqu’à Cordoue puis de Cordoue jusqu’en Hollande et c’est là que Leibnitz puis d’autres ont inventé le calcul numérique ».

IV. CONCLUSION

Plusieurs pièces à conviction permettent aujourd’hui de situer et dater l’origine des mathématiques : les figures géométriques de Bomblos (Afrique du Sud), datant de 77 000 ans ; l’os d’Ishango (Congo), datant de plus de 20 000 ans et considéré comme la première calculatrice de l’humanité ; les fractales qui reproduisent, selon des algorithmes très élaborées, la géométrie de la nature dans l’architecture, l’art, le textile, la coiffure, … ; le code binaire, utilisé dans les calculs et l’art de la divination ; avec du sable utilisaient un code binaire. Ces concepts et outils mathématiques pourraient ensuite avoir migré plus au nord où ils auraient rendu possible la construction des pyramides et édifices égyptiens. Ils pourraient également être à l’origine des algorithmes utilisés dans les ordinateurs modernes. Le travail des scientifiques travaillant sur ces sujets est une porte ouverte sur un lien à établir entre les traditions ancestrales africaines et la modernité scientifique. Ils devraient confirmer que l’Afrique noire a été une étape essentielle dans le long processus de la création de la pensée mathématique, avec pour aboutissement, les civilisations soudanaise puis égyptienne.